1. Analyzing Bubble Sort, Selection Sort, Insertion Sort
Algorithm Analysis
In order to compare two algorithms we need to come up with some measure that captures
their efficiency. One possibility is to simply generate lots of different sequences of
numbers, run both algorithms on each sequence, and record the actual execution time.
However, we need to be careful to run the algorithms on the same type of computer.
Also, this approach does not give us good understanding why one of the algorithms is
better than the other.
Another approach is to count the number of instructions carried out by each algorithm.
If we count carefully, we will gain good understanding about the actual operation of
the algorithms and will be able to explain in what circumstances one will be preferred
to the other.
It is tedious to count all instructions, so instead we will focus on the two most
important ones in the context of the sorting algorithms:
* the number of comparisons between two elements
* the number of swaps of two elements
We also need to consider whether certain types of configurations will lead to different
execution patterns. That is, will some configurations be "easy" for an algorithm (best-case
configurations), and will others be inherently "harder" (worst-case)?
Bubble Sort (Best Case)
The *best case* for Bubble Sort is when the input array is *already sorted*. In this case:
* # runs = 1 (we need only one run to confirm that no pair is out of order)
* # comparisons = n-1 (the first run needs to compare all pairs, and we have n-1 pairs)
* # swaps = 0 (no pair is found to be out of order, so no swaps)
Here is a visualization of the total number of operations for the *best case* of bubble sort:
 Bubble Sort (Worst Case)
The *worst case* for Bubble Sort is when the input array is *sorted in reverse*. In this case:
* # runs = n-1 (each run will put one element in its correct position; when the (n-1)st
element is placed in its correct spot, the n-th must also be in its correct spot)
* # comparisons
1st run: n-1 comparisons (examine all pairs)
2nd run: n-2 comparisons (examine all but the last pair)
3rd run: n-3 comparisons (examine all but the last 2 pairs)
...
(n-1)st run: n-(n-1) = 1 comparisons (examine all but the last n-1 pairs)
overall: (n-1) + (n-2) + (n-3) + ... + 1 = (n-1)*n / 2 or approx. n^2 / 2 comparisons
* # swaps
the number of swaps will be the same as the number of comparisons -- each comparison
will report that the current pair is out of order, which will lead to a swap
overall: (n-1)*n / 2 or approx. n^2 / 2 swaps
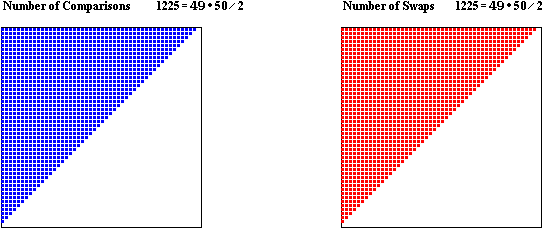
Here is a visualization of the total number of operations for the *worst case* of Bubble Sort:
Bubble Sort (Worst Case)
The *worst case* for Bubble Sort is when the input array is *sorted in reverse*. In this case:
* # runs = n-1 (each run will put one element in its correct position; when the (n-1)st
element is placed in its correct spot, the n-th must also be in its correct spot)
* # comparisons
1st run: n-1 comparisons (examine all pairs)
2nd run: n-2 comparisons (examine all but the last pair)
3rd run: n-3 comparisons (examine all but the last 2 pairs)
...
(n-1)st run: n-(n-1) = 1 comparisons (examine all but the last n-1 pairs)
overall: (n-1) + (n-2) + (n-3) + ... + 1 = (n-1)*n / 2 or approx. n^2 / 2 comparisons
* # swaps
the number of swaps will be the same as the number of comparisons -- each comparison
will report that the current pair is out of order, which will lead to a swap
overall: (n-1)*n / 2 or approx. n^2 / 2 swaps
Here is a visualization of the total number of operations for the *worst case* of Bubble Sort:
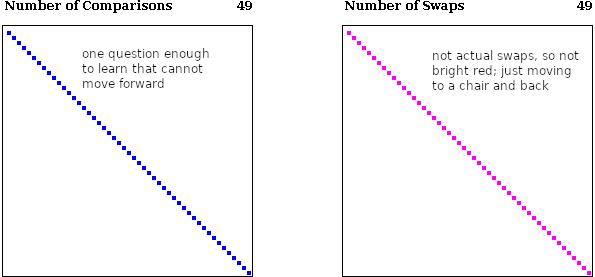
 Insertion Sort (Best Case)
The *best case* for Insertion Sort is when the input array is *already sorted*. Remember
the airport analogy: each person tries to move to the front of the line, by asking those
in front about the time of their flight. But if the line is already ordered, each person
finds out after one question that there is no need to move.
Also, since the line is already sorted, no swaps take place.
* # comparisons = n-1 (each item compares itself with the one in front and discovers
that there is no need to move forward, so one question per item)
* # swaps = n-1 (no pair is found to be out of order, so no swaps; however, each
element temporarily leaves and comes back for 1 unit of work)
Here is a visualization of the total number of operations for the *best case* of insertion sort:
Insertion Sort (Best Case)
The *best case* for Insertion Sort is when the input array is *already sorted*. Remember
the airport analogy: each person tries to move to the front of the line, by asking those
in front about the time of their flight. But if the line is already ordered, each person
finds out after one question that there is no need to move.
Also, since the line is already sorted, no swaps take place.
* # comparisons = n-1 (each item compares itself with the one in front and discovers
that there is no need to move forward, so one question per item)
* # swaps = n-1 (no pair is found to be out of order, so no swaps; however, each
element temporarily leaves and comes back for 1 unit of work)
Here is a visualization of the total number of operations for the *best case* of insertion sort:
 Insertion Sort (Worst Case)
The *worst case* for Insertion Sort is when the input array is *sorted in reverse*. Using
the airport analogy: each person tries to move to the front of the line, by asking those
in front about the time of their flight. In this case, each person discovers that everyone
in front has a later flight, so each person will walk from their current position to the
front of the line.
Unlike the *best case* this time each person will swap with everyone that is currently in
front, so there will be many more swaps.
* # questions/comparisons:
0-th person ignored, since they are at the from of the line
1-st person will ask 1 question (only one other person in front)
2-nd person will ask 2 questions (since everyone in front has later flight)
3-rd person will ask 3 questions (since everyone in front has later flight)
...
(n-1)-th will ask n-1 questions (since everyone in front has later flight)
overall: 1 + 2 + 3 + ... + n-1 = (n-1)*n / 2 or approx. n^2 / 2 # questions/comparisons
* # swaps:
Since each question will lead to people changing places, the total number of
swaps is the same as the total number of questions/comparisons:
overall: (n-1)*n / 2 or approx. n^2 / 2 #swaps (= # comparisons)
Here is a visualization of the total number of operations for the *worst case* of Insertion Sort:
Insertion Sort (Worst Case)
The *worst case* for Insertion Sort is when the input array is *sorted in reverse*. Using
the airport analogy: each person tries to move to the front of the line, by asking those
in front about the time of their flight. In this case, each person discovers that everyone
in front has a later flight, so each person will walk from their current position to the
front of the line.
Unlike the *best case* this time each person will swap with everyone that is currently in
front, so there will be many more swaps.
* # questions/comparisons:
0-th person ignored, since they are at the from of the line
1-st person will ask 1 question (only one other person in front)
2-nd person will ask 2 questions (since everyone in front has later flight)
3-rd person will ask 3 questions (since everyone in front has later flight)
...
(n-1)-th will ask n-1 questions (since everyone in front has later flight)
overall: 1 + 2 + 3 + ... + n-1 = (n-1)*n / 2 or approx. n^2 / 2 # questions/comparisons
* # swaps:
Since each question will lead to people changing places, the total number of
swaps is the same as the total number of questions/comparisons:
overall: (n-1)*n / 2 or approx. n^2 / 2 #swaps (= # comparisons)
Here is a visualization of the total number of operations for the *worst case* of Insertion Sort:
Note: This analysis shows that Bubble Sort and Insertion Sort do the same amount of
work in *worst case* configurations. However, recall that Insertion Sort does not do
true swaps, i.e. it does not swap two elements, but simply moves one to the right, so
each swap of insertions sort does half the work of a swap in Bubble Sort.
Thus, we would expect Insertions Sort to be faster than Bubble Sort when the items
are ordered in reverse.
When the items are already sorted Bubble Sort might have a slight advantage, since
no swaps take place, but Insertions Sort still temporarily moves the current element
to the side before bringing it back.
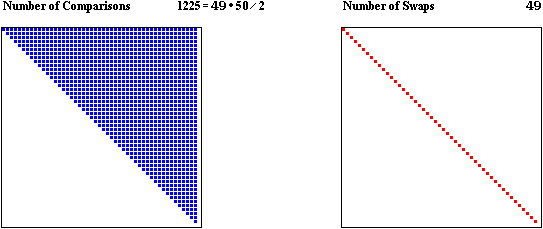
Selection Sort (Best Case)
The *best case* for Selection Sort is when the input array is *already sorted*. In this case:
* # passes = n-1 (as in bubble sort, each pass will put one element in its correct position)
* # comparisons
1st pass: n-1 comparisons (n-2 to find smallest among last (n-1) elements + 1 to compare with 1st element)
2nd pass: n-2 comparisons (n-3 to find smallest among last (n-2) elements + 1 to compare with 2st element)
3rd pass: n-3 comparisons (n-4 to smallest among last (n-3) elements and compare with 3rd element)
...
(n-1)st pass: 1 comparisons (compare the last pair)
overall: (n-1) + (n-2) + (n-3) + ... + 1 = (n-1)*n / 2 or approx. n^2 / 2 comparisons
* # swaps
unlike Bubble Sort, selection sort makes *at most one swap* per pass -- this happens
when the current element is bigger than the smallest one to the right of it
since the array is already sorted, no swap will be required
overall: 0 swaps
Here is a visualization of the total number of operations for the *best case* of selection sort:
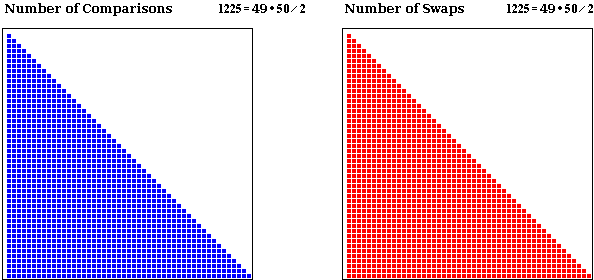
 Selection Sort (Worst Case)
The *worst case* for selection sort is when the input array is *sorted in reverse*. The details of
the analysis are the same as in the analysis for the *best case*. The only difference is that each
pass will make 1 swap (i.e. will discover that current element is bigger than the smallest one to
the right of it.
Overall, we get:
* # passes = n-1
* # comparisons = (n-1)*n / 2 or approx n^2 / 2
* # swaps = n-1 (1 swap per pass)
Here is a visualization of the total number of operations for the *worst case* of selection sort:
Selection Sort (Worst Case)
The *worst case* for selection sort is when the input array is *sorted in reverse*. The details of
the analysis are the same as in the analysis for the *best case*. The only difference is that each
pass will make 1 swap (i.e. will discover that current element is bigger than the smallest one to
the right of it.
Overall, we get:
* # passes = n-1
* # comparisons = (n-1)*n / 2 or approx n^2 / 2
* # swaps = n-1 (1 swap per pass)
Here is a visualization of the total number of operations for the *worst case* of selection sort:
 Summary (Visualization based on project at Smith College)
Summary (Visualization based on project at Smith College)
| Best Case (n = 50) |
Worst Case (n = 50) |
Bubble Sort
(n = 50) |

|
Insertion Sort
(n = 50) |

|
Selection Sort
(n = 50) |

|
|
|
Bubble Sort (Worst Case) The *worst case* for Bubble Sort is when the input array is *sorted in reverse*. In this case: * # runs = n-1 (each run will put one element in its correct position; when the (n-1)st element is placed in its correct spot, the n-th must also be in its correct spot) * # comparisons 1st run: n-1 comparisons (examine all pairs) 2nd run: n-2 comparisons (examine all but the last pair) 3rd run: n-3 comparisons (examine all but the last 2 pairs) ... (n-1)st run: n-(n-1) = 1 comparisons (examine all but the last n-1 pairs) overall: (n-1) + (n-2) + (n-3) + ... + 1 = (n-1)*n / 2 or approx. n^2 / 2 comparisons * # swaps the number of swaps will be the same as the number of comparisons -- each comparison will report that the current pair is out of order, which will lead to a swap overall: (n-1)*n / 2 or approx. n^2 / 2 swaps Here is a visualization of the total number of operations for the *worst case* of Bubble Sort:
Insertion Sort (Best Case) The *best case* for Insertion Sort is when the input array is *already sorted*. Remember the airport analogy: each person tries to move to the front of the line, by asking those in front about the time of their flight. But if the line is already ordered, each person finds out after one question that there is no need to move. Also, since the line is already sorted, no swaps take place. * # comparisons = n-1 (each item compares itself with the one in front and discovers that there is no need to move forward, so one question per item) * # swaps = n-1 (no pair is found to be out of order, so no swaps; however, each element temporarily leaves and comes back for 1 unit of work) Here is a visualization of the total number of operations for the *best case* of insertion sort:
Insertion Sort (Worst Case) The *worst case* for Insertion Sort is when the input array is *sorted in reverse*. Using the airport analogy: each person tries to move to the front of the line, by asking those in front about the time of their flight. In this case, each person discovers that everyone in front has a later flight, so each person will walk from their current position to the front of the line. Unlike the *best case* this time each person will swap with everyone that is currently in front, so there will be many more swaps. * # questions/comparisons: 0-th person ignored, since they are at the from of the line 1-st person will ask 1 question (only one other person in front) 2-nd person will ask 2 questions (since everyone in front has later flight) 3-rd person will ask 3 questions (since everyone in front has later flight) ... (n-1)-th will ask n-1 questions (since everyone in front has later flight) overall: 1 + 2 + 3 + ... + n-1 = (n-1)*n / 2 or approx. n^2 / 2 # questions/comparisons * # swaps: Since each question will lead to people changing places, the total number of swaps is the same as the total number of questions/comparisons: overall: (n-1)*n / 2 or approx. n^2 / 2 #swaps (= # comparisons) Here is a visualization of the total number of operations for the *worst case* of Insertion Sort:
 Note: This analysis shows that Bubble Sort and Insertion Sort do the same amount of work in *worst case* configurations. However, recall that Insertion Sort does not do true swaps, i.e. it does not swap two elements, but simply moves one to the right, so each swap of insertions sort does half the work of a swap in Bubble Sort. Thus, we would expect Insertions Sort to be faster than Bubble Sort when the items are ordered in reverse. When the items are already sorted Bubble Sort might have a slight advantage, since no swaps take place, but Insertions Sort still temporarily moves the current element to the side before bringing it back.Selection Sort (Best Case) The *best case* for Selection Sort is when the input array is *already sorted*. In this case: * # passes = n-1 (as in bubble sort, each pass will put one element in its correct position) * # comparisons 1st pass: n-1 comparisons (n-2 to find smallest among last (n-1) elements + 1 to compare with 1st element) 2nd pass: n-2 comparisons (n-3 to find smallest among last (n-2) elements + 1 to compare with 2st element) 3rd pass: n-3 comparisons (n-4 to smallest among last (n-3) elements and compare with 3rd element) ... (n-1)st pass: 1 comparisons (compare the last pair) overall: (n-1) + (n-2) + (n-3) + ... + 1 = (n-1)*n / 2 or approx. n^2 / 2 comparisons * # swaps unlike Bubble Sort, selection sort makes *at most one swap* per pass -- this happens when the current element is bigger than the smallest one to the right of it since the array is already sorted, no swap will be required overall: 0 swaps Here is a visualization of the total number of operations for the *best case* of selection sort:
Note: This analysis shows that Bubble Sort and Insertion Sort do the same amount of work in *worst case* configurations. However, recall that Insertion Sort does not do true swaps, i.e. it does not swap two elements, but simply moves one to the right, so each swap of insertions sort does half the work of a swap in Bubble Sort. Thus, we would expect Insertions Sort to be faster than Bubble Sort when the items are ordered in reverse. When the items are already sorted Bubble Sort might have a slight advantage, since no swaps take place, but Insertions Sort still temporarily moves the current element to the side before bringing it back.Selection Sort (Best Case) The *best case* for Selection Sort is when the input array is *already sorted*. In this case: * # passes = n-1 (as in bubble sort, each pass will put one element in its correct position) * # comparisons 1st pass: n-1 comparisons (n-2 to find smallest among last (n-1) elements + 1 to compare with 1st element) 2nd pass: n-2 comparisons (n-3 to find smallest among last (n-2) elements + 1 to compare with 2st element) 3rd pass: n-3 comparisons (n-4 to smallest among last (n-3) elements and compare with 3rd element) ... (n-1)st pass: 1 comparisons (compare the last pair) overall: (n-1) + (n-2) + (n-3) + ... + 1 = (n-1)*n / 2 or approx. n^2 / 2 comparisons * # swaps unlike Bubble Sort, selection sort makes *at most one swap* per pass -- this happens when the current element is bigger than the smallest one to the right of it since the array is already sorted, no swap will be required overall: 0 swaps Here is a visualization of the total number of operations for the *best case* of selection sort:Selection Sort (Worst Case) The *worst case* for selection sort is when the input array is *sorted in reverse*. The details of the analysis are the same as in the analysis for the *best case*. The only difference is that each pass will make 1 swap (i.e. will discover that current element is bigger than the smallest one to the right of it. Overall, we get: * # passes = n-1 * # comparisons = (n-1)*n / 2 or approx n^2 / 2 * # swaps = n-1 (1 swap per pass) Here is a visualization of the total number of operations for the *worst case* of selection sort:
Summary (Visualization based on project at Smith College)